Publications

We introduce a machine-learning framework to warm-start fixed-point optimization algorithms. Our architecture consists of a neural network mapping problem parameters to warm starts, followed by a predefined number of fixed-point iterations. We propose two loss functions designed to either minimize the fixed-point residual or the distance to a ground truth solution. In this way, the neural network predicts warm starts with the end-to-end goal of minimizing the downstream loss. An important feature of our architecture is its flexibility, in that it can predict a warm start for fixed-point algorithms run for any number of steps, without being limited to the number of steps it has been trained on. We provide PAC-Bayes generalization bounds on unseen data for common classes of fixed-point operators: contractive, linearly convergent, and averaged. Applying this framework to well-known applications in control, statistics, and signal processing, we observe a significant reduction in the number of iterations and solution time required to solve these problems, through learned warm starts.

@article{JMLR:v25:23-1174,
  author  = {Rajiv Sambharya and Georgina Hall and Brandon Amos and Bartolomeo Stellato},
  title   = {Learning to Warm-Start Fixed-Point Optimization Algorithms},
  journal = {Journal of Machine Learning Research},
  year    = {2024},
  volume  = {25},
  number  = {166},
  pages   = {1--46},
  url     = {http://jmlr.org/papers/v25/23-1174.html}
}
}

First-order methods are widely used to solve convex quadratic programs (QPs) in real-time applications because of their low per-iteration cost. However, they can suffer from slow convergence to accurate solutions. In this paper, we present a framework which learns an effective warm-start for a popular first-order method in real-time applications, Douglas-Rachford (DR) splitting, across a family of parametric QPs. This framework consists of two modules: a feedforward neural network block, which takes as input the parameters of the QP and outputs a warm-start, and a block which performs a fixed number of iterations of DR splitting from this warm-start and outputs a candidate solution. A key feature of our framework is its ability to do end-to-end learning as we differentiate through the DR iterations. To illustrate the effectiveness of our method, we provide generalization bounds (based on Rademacher complexity) that improve with the number of training problems and number of iterations simultaneously. We further apply our method to three real-time applications and observe that, by learning good warm-starts, we are able to significantly reduce the number of iterations required to obtain high-quality solutions.

@misc{sambharya_2022_endtoend,
      title={End-to-End Learning to Warm-Start for Real-Time Quadratic Optimization}, 
      author={Rajiv Sambharya and Georgina Hall and Brandon Amos and Bartolomeo Stellato},
      year={2022},
      eprint={2212.08260},
      archivePrefix={arXiv},
      primaryClass={math.OC}
}

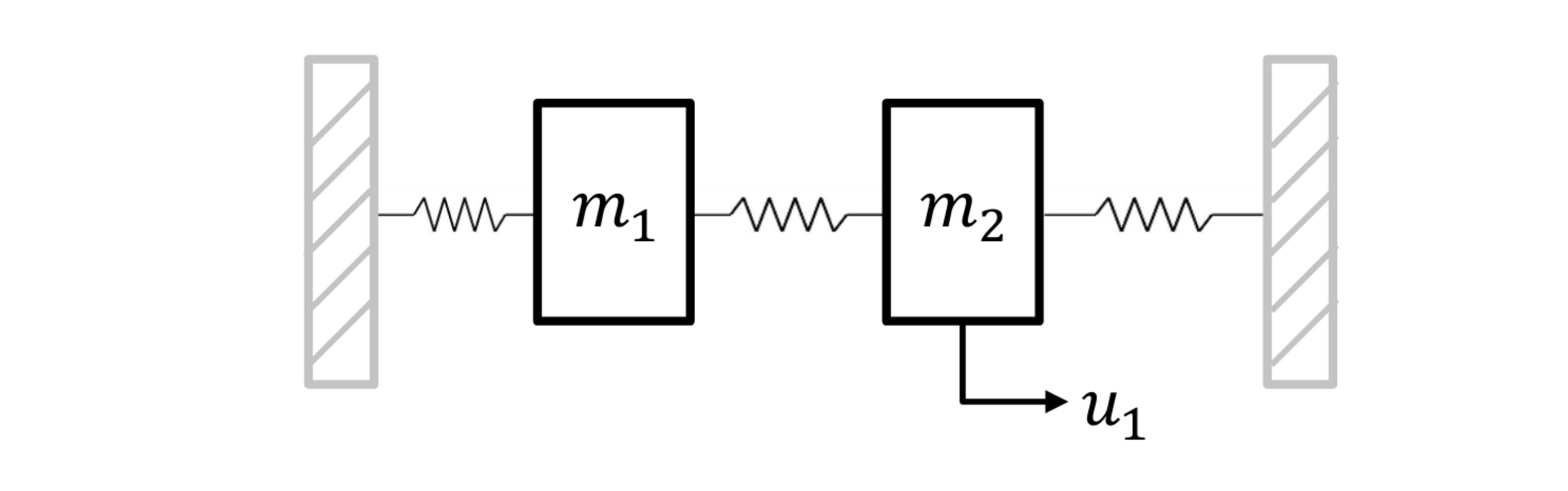
Consider a system of many masses and springs where the masses have actuators that we can control. The goal is to control the system so that it tracks a reference trajectory. Specifically, we aim to solve the convex optimization problem,

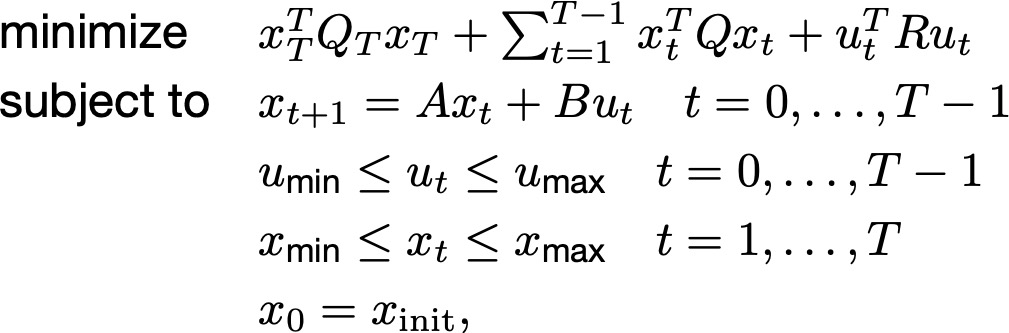
where the $x_t$’s are the states and the $u_t$’s are the controls.

In the model predictive control paradigm, we solve this problem for some horizon length and implement the first control, $u_0$. After this, we resolve the problem where only the initial state parameter, $\theta = x_{\rm{init}}$, changes. Since we need to solve this problem many times, we will have an abundance of data to use. Standard optimization techniques don’t capitalize on this data. In our work, we learn a good warm-start for Douglas-Rachford (DR) splitting from this data.

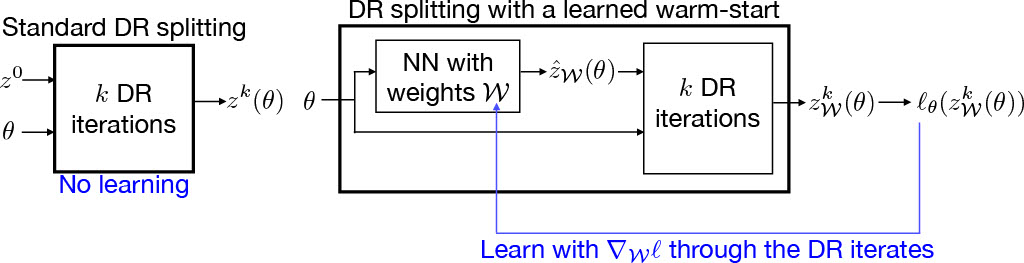
Left: standard DR splitting which maps parameter $\theta$ and initialization $z^0$ to an approximate solution $z^k(\theta)$. Right: Proposed learning framework consisting of two modules. The first module is the neural network (NN) block which maps the parameter $\theta$ to a warm-start $z^k_{\mathcal{W}}(\theta)$. The weights of the NN, denoted by $\mathcal{W}$, are the only variables we optimize over. The second module runs $k$ iterations of DR splitting (which also depend on $\theta$) starting with the warm-start $z^k_{\mathcal{W}}(\theta)$ and returning a candidate solution $z^k_{\mathcal{W}}(\theta)$. We backpropagate from the loss $\ell_{\theta}(z^k_{\mathcal{W}}(\theta))$ through the DR iterates to learn the optimal weights $\mathcal{W}$.

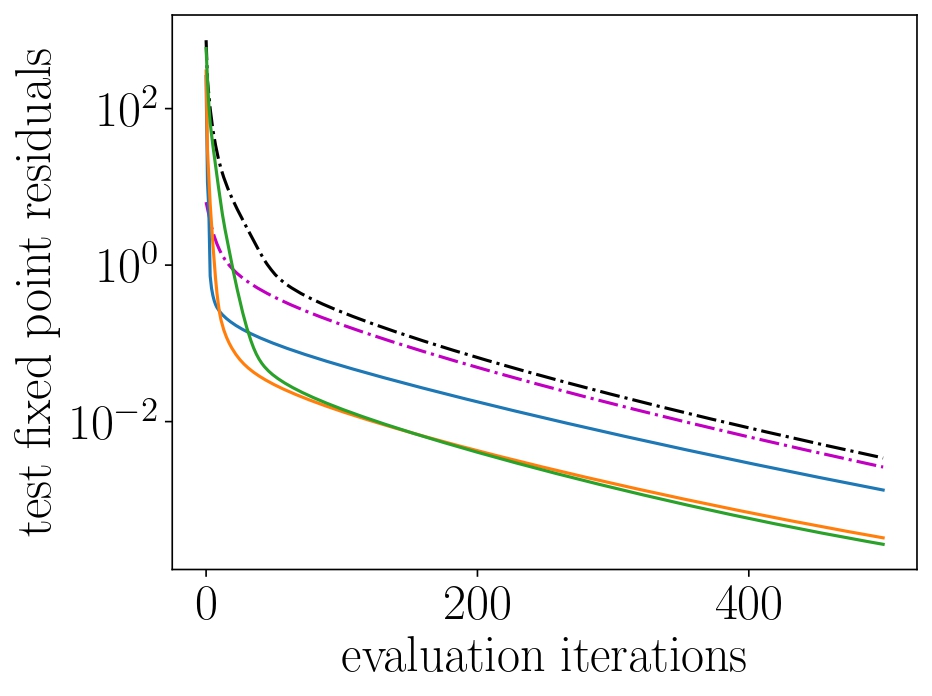
o no warm-start o nearest neighbor warm-start

learned warm-start with $k = $ { o $5$ o $15$ o $50$ }

We plot the test fixed point residuals for different warm-starts of DR splitting. We train our architecture with $k=5,15,$ and $50$ DR iterations. We compare our results against a random initialization (black) and against warm-starting DR splitting with the nearest neighbor from the train set (magenta). We combine operator theory and Rademacher complexity theory to provide generalization bounds that depend on both the number of evaluation iterations, $k$ and the number of training problems.

We introduce a data-driven approach to analyze the performance of continuous optimization algorithms using generalization guarantees from statistical learning theory. We study classical and learned optimizers to solve families of parametric optimization problems. We build generalization guarantees for classical optimizers, using a sample convergence bound, and for learned optimizers, using the Probably Approximately Correct (PAC)-Bayes framework. To train learned optimizers, we use a gradient-based algorithm to directly minimize the PAC-Bayes upper bound. Numerical experiments in signal processing, control, and meta-learning showcase the ability of our framework to provide strong generalization guarantees for both classical and learned optimizers given a fixed budget of iterations. For classical optimizers, our bounds are much tighter than those that worst-case guarantees provide. For learned optimizers, our bounds outperform the empirical outcomes observed in their non-learned counterparts.

@misc{sambharya2024datadriven,
      title={Data-Driven Performance Guarantees for Classical and Learned Optimizers}, 
      author={Rajiv Sambharya and Bartolomeo Stellato},
      year={2024},
      eprint={2404.13831},
      archivePrefix={arXiv},
      primaryClass={math.OC}
}

We describe a novel family of models of multi- layer feedforward neural networks in which the activation functions are encoded via penalties in the training problem. Our approach is based on representing a non-decreasing activation function as the argmin of an appropriate convex optimization problem. The new framework allows for algorithms such as block-coordinate descent methods to be applied, in which each step is composed of a simple (no hidden layer) supervised learning problem that is parallelizable across data points and/or layers. Experiments indicate that the pro- posed models provide excellent initial guesses for weights for standard neural networks. In addition, the model provides avenues for interesting extensions, such as robustness against noisy in- puts and optimizing over parameters in activation functions.

@misc{askari_lifted_nn,
  doi = {10.48550/ARXIV.1805.01532},
  url = {https://arxiv.org/abs/1805.01532},
  author = {Askari, Armin and Negiar, Geoffrey and Sambharya, Rajiv and Ghaoui, Laurent El},
  keywords = {Machine Learning (cs.LG), Machine Learning (stat.ML), FOS: Computer and information sciences, FOS: Computer and information sciences},
  title = {Lifted Neural Networks},
  publisher = {arXiv},
  year = {2018},
  copyright = {Creative Commons Attribution Share Alike 4.0 International}
}